Rafter Lengths
Rafter Lengths
Have you ever wanted to know how to work out the rafter length for your roof?
Here are two ways you can do this by applying a little bit of maths depending on what facts you already know.
Method 1 – You know both the rise and run
The simplest way is to use Pythagoras’ Theorem which we have already written about here. Mathematically the rafter length, c, is found using the following equation:

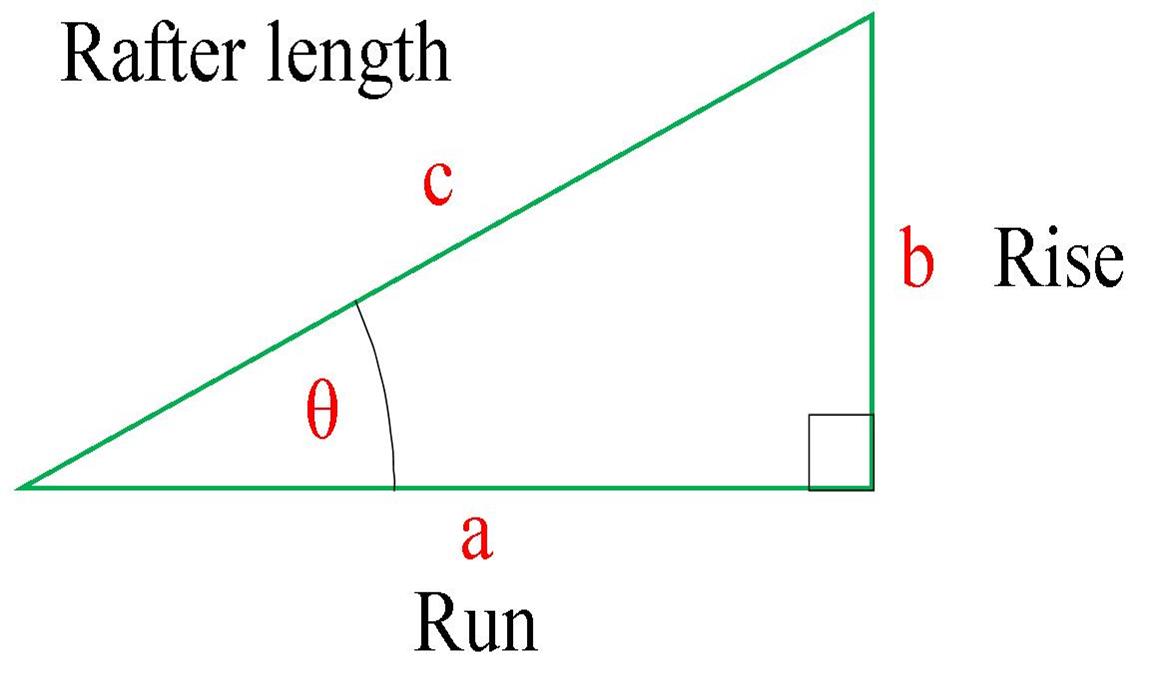
For example. Rise = 1.8m, Run = 2.4m
Rafter length = √ [ (2.4)2 + (1.8)2 ] = 3.0m
The eagle-eyed will have spoted this is another example of a 3-4-5 triangle.
Method 2 – You know the roof pitch, θ, and the rise or the run.
Using a bit of trigonometry you can find the rafter length using the following equations.
Rafter length = Run ÷ cos θ = Rise ÷ sin θ
For example. Run = 2.4m, roof pitch = 45°
Rafter length = 2.4 ÷ cos(45°) = 3.39m to 2 d.p.
Any modern mobile phone will be able to perform these calculations.
There is a useful table below for your convenience.
Just multiply the rise or run by the appropriate rafter length factor corresponding to your roof pitch.
For example, if your roof pitch is 30ﹾ and your run is 2.4m then reading from the table the rafter length factor is 1.15. Multiply this factor by your run which gives your rafter length. If you want to add on a rafter foot (overhang) add this to your rafter length.
( 2.4 x 1.15 ) + 0.45 = 3.21 metre
Run Factor Overhang Rafter length
| Roof Pitch | |||||||||||
| 10ﹾ | 15ﹾ | 20ﹾ | 25ﹾ | 30ﹾ | 35ﹾ | 40ﹾ | 45ﹾ | 50ﹾ | 55ﹾ | 60ﹾ | |
| Rafter factor for rise (to 2 d.p.) | 5.76 | 3.86 | 2.92 | 2.37 | 2.00 | 1.74 | 1.56 | 1.41 | 1.31 | 1.22 | 1.15 |
| Rafter factor for run (to 2 d.p.) | 1.02 | 1.04 | 1.06 | 1.10 | 1.15 | 1.22 | 1.31 | 1.41 | 1.56 | 1.74 | 2.00 |
